Contact-Aided Navigation of Tendon-driven Continuum Robots

One of the most predominant features of tendon-driven continuum robots is their compliance. These ‘bendy’ flexible robots are widely used for their ability to conform to curvilinear shapes in response to forces applied by varied actuation. The most common actuation is the straight tendon routing (where the tendons run in a straight path, parallel to the backbone). In a hand-wavy approximation, this actuation can be assumed to apply a constant moment throughout the backbone, resulting in a constant curvature (also explained in a previous blogpost. Introducing changes in the routing patterns¹ or adding mechanisms² results in additional forces/moments in the system, resulting in non-constant curvature along a single segment.

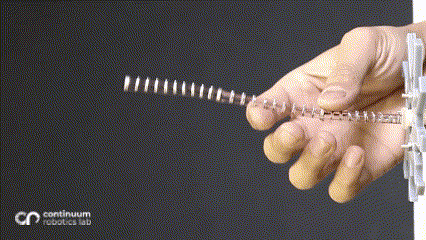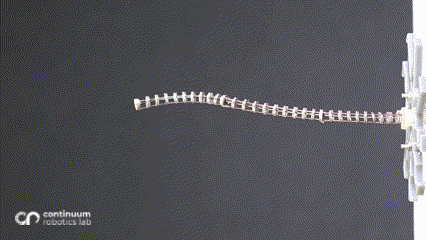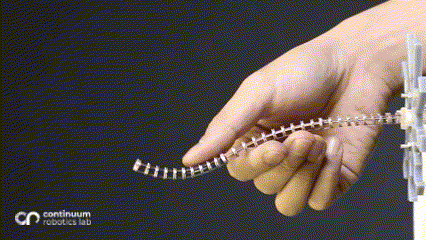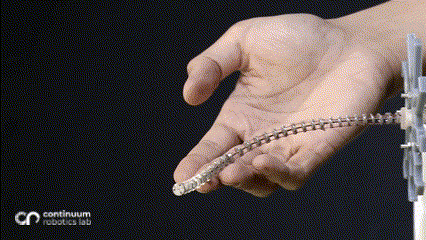
While changing the robot design mechanically is viable, we asked ourselves whether we can harness more from the traditional single segment straight routing design to achieve more variation than just a constant-curvature. What if these additional forces/moments came from the environment instead of mechanical additions - which would be possible if the robot now leveraged the obstacles to change its curvature? This idea inspired our research on contact-aided navigation for these robots.

Reaching a target

Let’s consider a single segment TDCR in a planar workspace, cluttered with obstacles marked in blue. If the robot tip needs to reach the target position (red dot in the animation below), it is a fairly simple task. You basically need to select actutation values that minimize the distance between the tip and the target. We can set up a simple joint space search for this - where we consider three possible actions:

1. segment length increase (as its inserted into the workspace),
2. tendon length decrease, and
3. tendon length increase.

Starting from an initial joint value, these three actions can be sequentially applied to build a lattice-based representation of the configuration space.

A lattice is a discretization of the configuration space into a set of states, and connections between these states, where every connection represents a feasible path.³

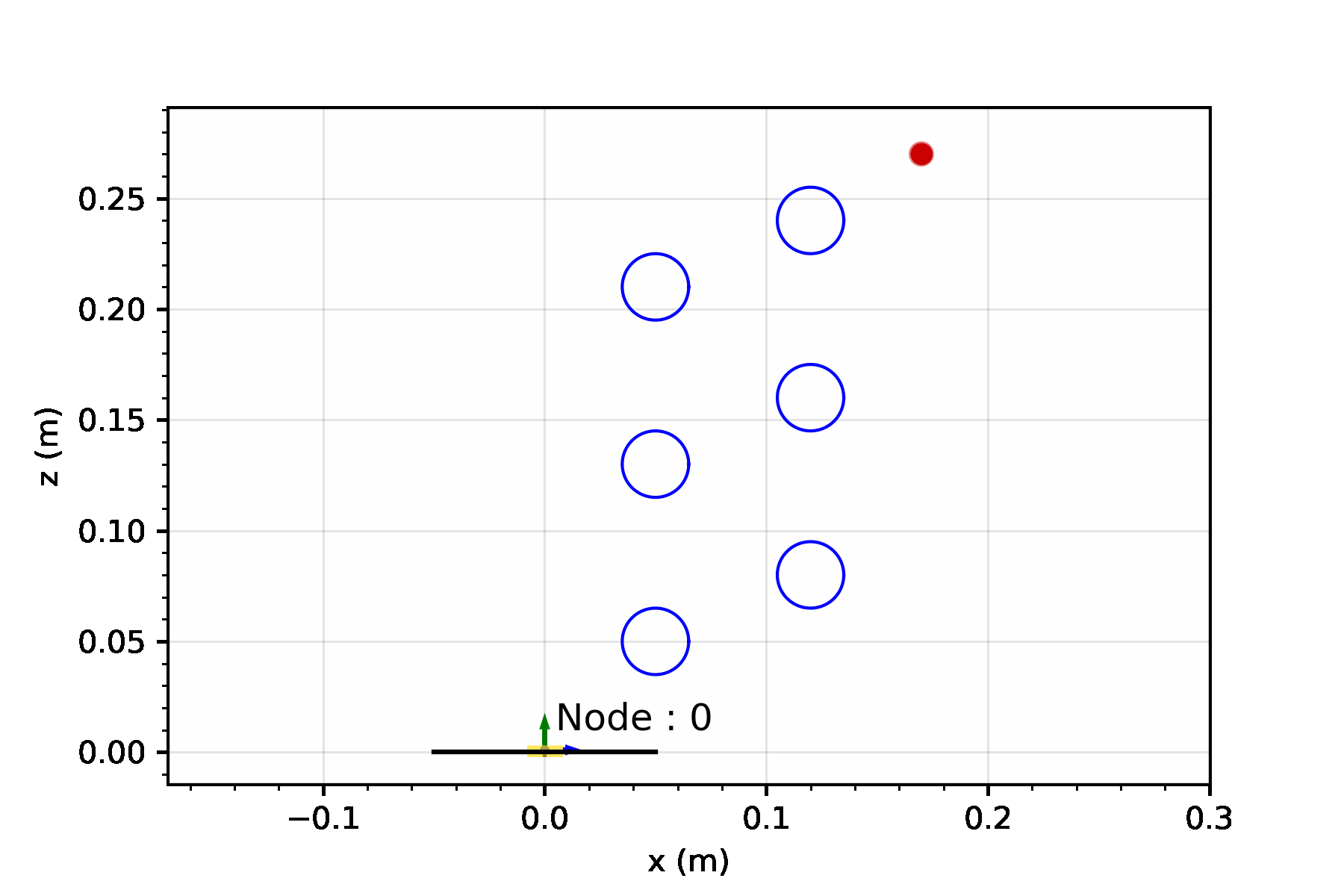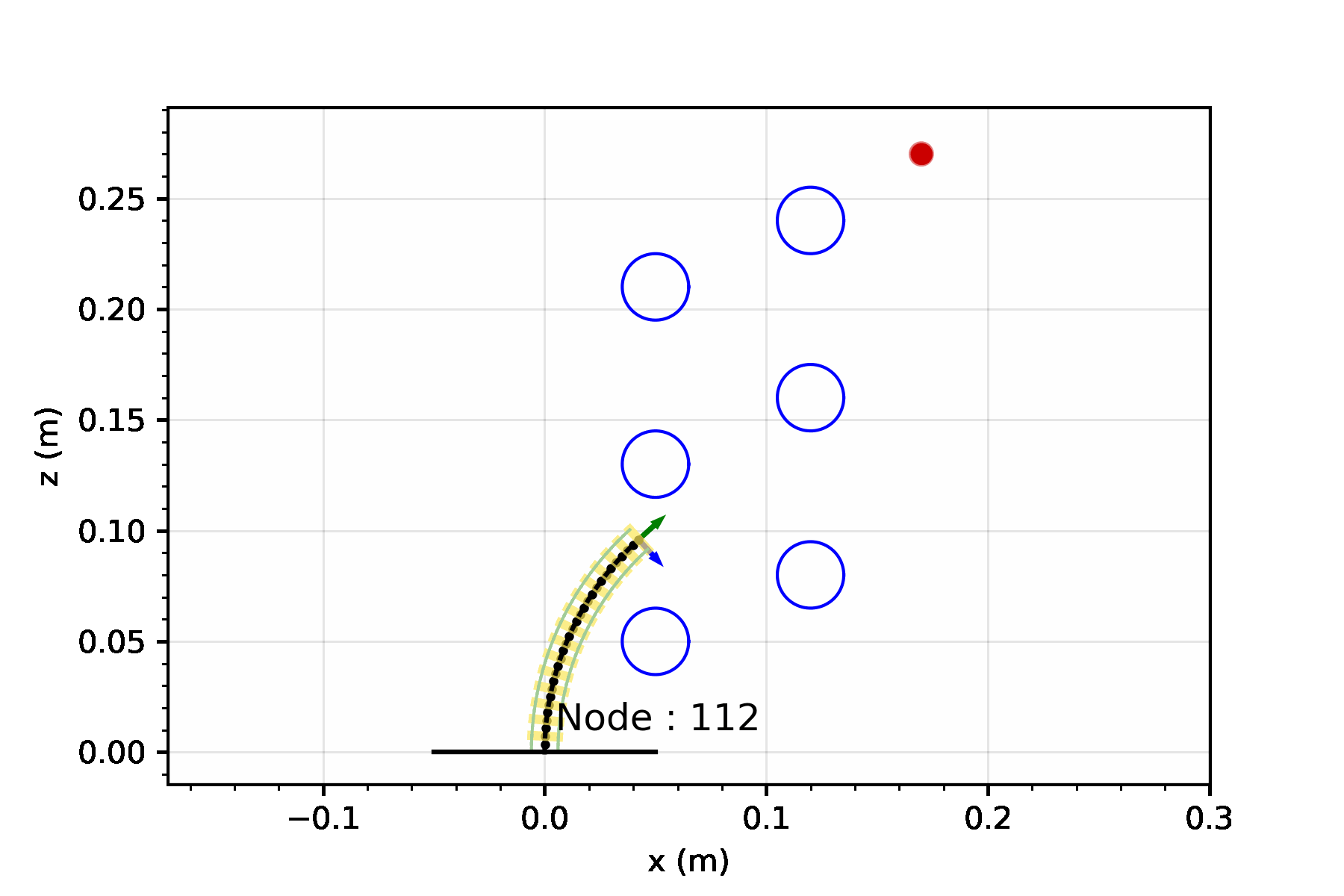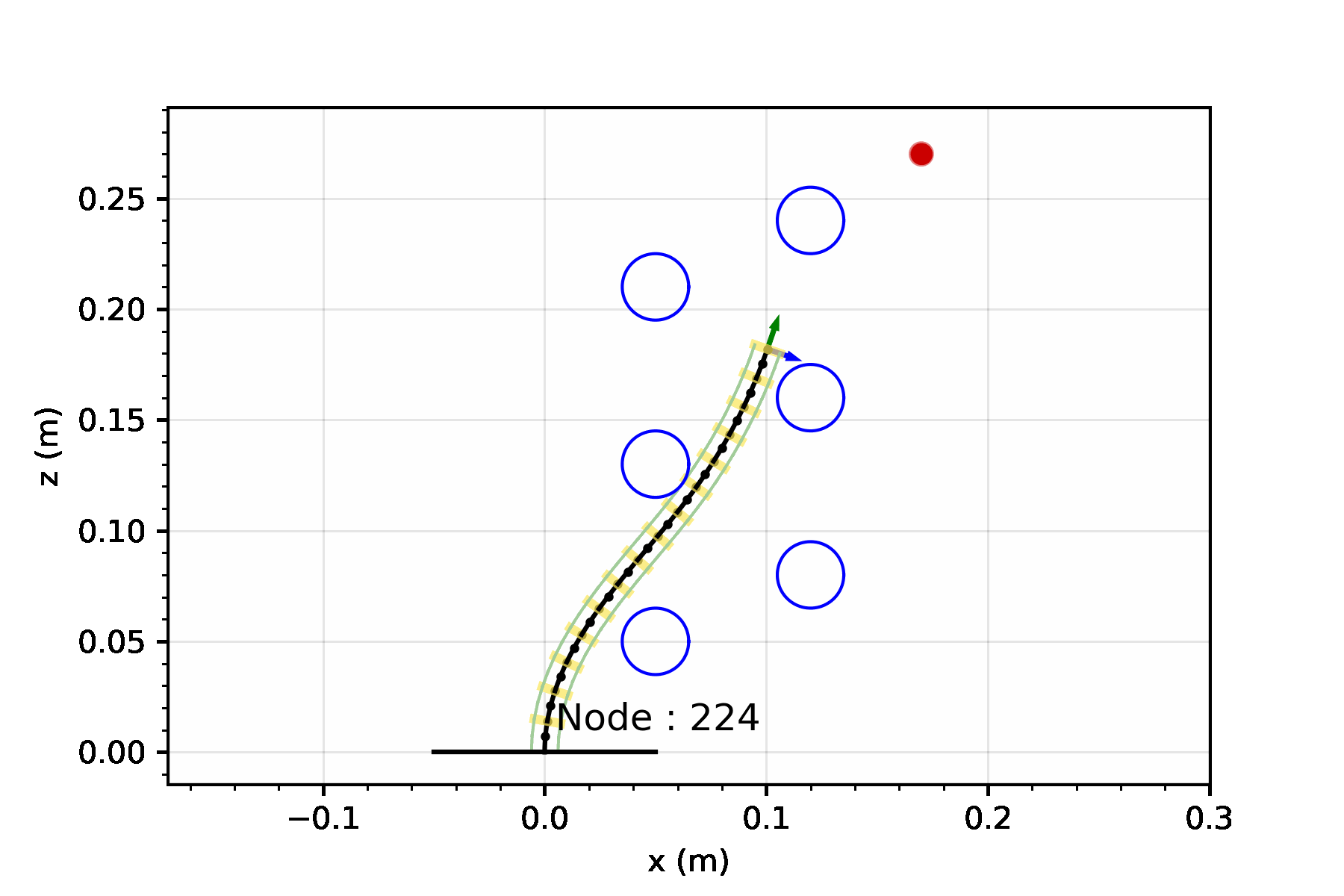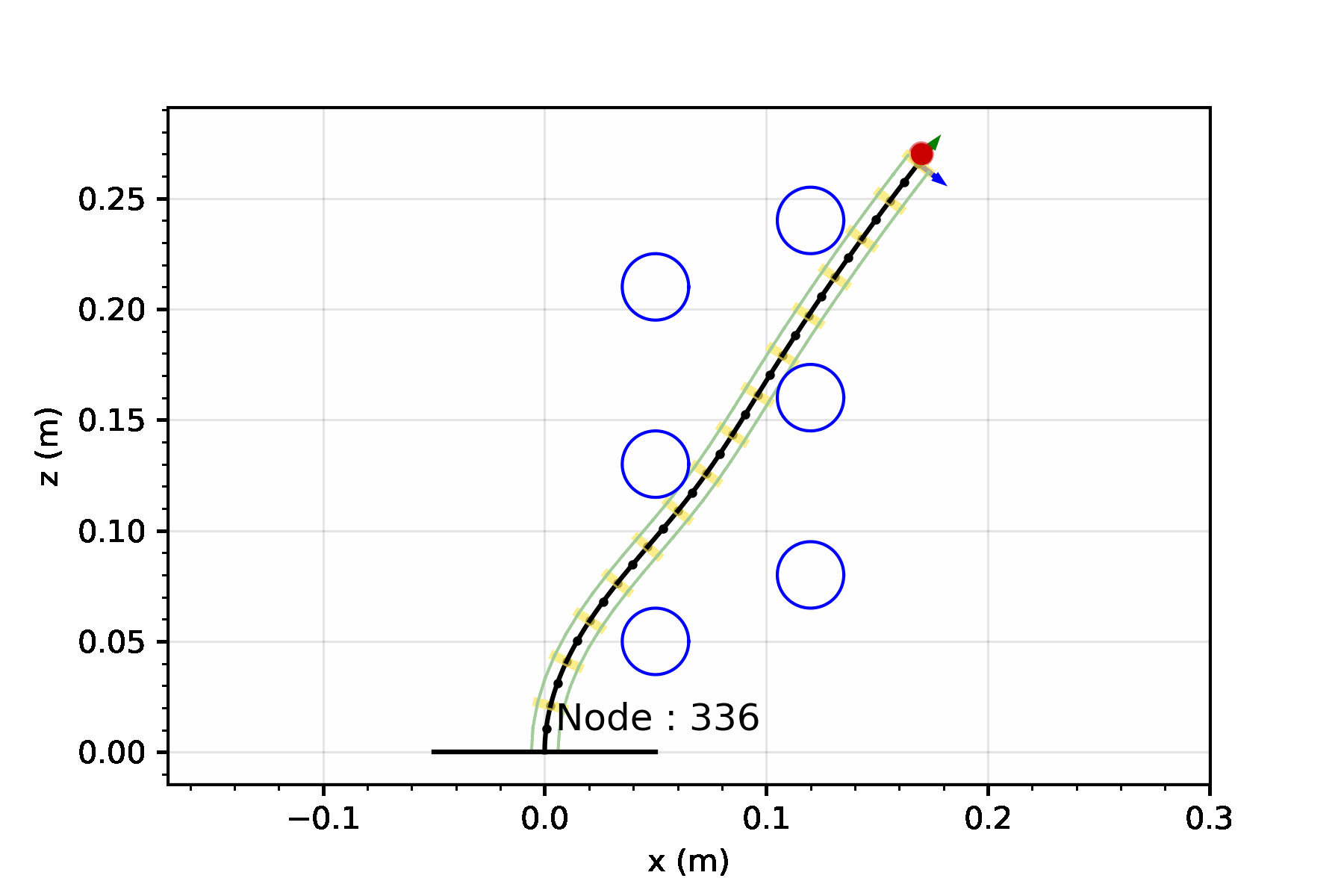
For now, lets keep optimality aside and focus on finding a solution by performing a greedy search. The greedy search is guided by a heuristic - for our case, we can set this heuristic to simply be the Euclidean distance between the robot tip and the target. This simple heuristic works quite well! There some additional changes you can make to prevent it from getting stuck in minimas but we will leave that discussion for another day.

Reaching a target pose

Now that we have a solution to reach a target position, we can add an additional layer of challenge to our problem - How can we reach a target, with not just the desired position, but a desired orientation as well? We can retain all the machinery from the previous section, of building a lattice in the configuration space by sequentially applying joint space actions. But the more important question we need to answer is:

What would the heuristic look like to reach a target pose?

To reach a desired pose, we need to control x, y, and theta of the tip. However, we only have two controllable degrees-of-freedom where we can either change the length of the segment or bend it. The single segment is essentially underactuated for this task - leveraging contact-aided navigation allows the segment to use the obstacle as a kind-of passive degree of freedom to control the tip.

Our work, recently published in the IEEE Robotics & Automation Letters⁴, seeks to solve this problem. The heuristic basically assumes that the end-effector’s motion can be modeled as a series of constant-curvature arcs - arcs whose end-points can only lie on the surface of obstacles. This condition ensures that the use of obstacles as a degree of freeodm is captured by the heuristic.

You can watch some of the solutions found by our method in the video below :

Open-Source materials

For now, we are releasing a preliminary version of the TDCR that can account for contacts on GitHub (link below). It is based on the kinematic model proposed by Ashwin et al. ⁵.

Please watch this space for more details and tutorials!

Paper GitHub Video

References

1. R.M. Grassmann, P. Rao, Q. Peyron, J. Burgner-Kahrs: FAS—A Fully Actuated Segment for Tendon-Driven Continuum Robots. Frontiers in Robotocs and AI, 9:873446, 2022. doi: 10.3389/frobt.2022.873446 ↩

2. P. Rao, C. Pogue, Q. Peyron, E. Diller, J. Burgner-Kahrs: Modeling and Analysis of Tendon-Driven Continuum Robots for Rod-Based Locking. IEEE Robotics & Automation Letters, 8(6):3126 - 3133, 2023. doi: 10.1109/LRA.2023.3264869 ↩

3. B. J. Cohen, G. Subramania, S. Chitta, M. Likhachev: Planning for Manipulation with Adaptive Motion Primitives. IEEE International Conference on Robotics and Automation, pp. 5478-5485, 2011. doi: 10.1109/ICRA.2011.5980550 ↩

4. P. Rao, O. Salzmann, J. Burgner-Kahrs: Towards Contact-Aided Motion Planning for Tendon-Driven Continuum Robots. IEEE Robotics & Automation Letters, 2024. doi: 10.1109/LRA.2024.3383211 ↩

5. K.P. Ashwin, Soumya Kanti Mahapatra, Ashitava Ghosal: Profile and contact force estimation of cable-driven continuum robots in presence of obstacles. Mechanism and Machine Theory, 164:104404, 2021. doi: 10.1016/j.mechmachtheory.2021.104404 ↩